Problem definition
* 대부분의 Post Training Quantization 방법들은 simulated quantization을 활용한다, 연산은 dequantize 후 fp
* integer-only inference 한다면 효율적인 efficient integer arithmetic unit을 극한으로 활용 가능할 것 + edge processor
* 기존 Integer-only method는 CNN, ViT나 Bert 같은 작은 트랜스포머 모델에 제한됨, SwiGLU나 RMSNorm 같은 복잡한 비선형 연산을 다루기는 부족 => 요즘 나오는 트랜스포머 기반 거대 LLM ?

* per-channel, per-token 으로 보면 값이 많이 튄다, 특히 non-linear 직후의 activation이 그렇더라, smoothing 없이 무작정 quantize하는 건 정확도에 치명적인 영향을 미친다
그래서 이 논문은 크게
- Fully-Smooth Block-Reconstruction (FSBR) => channel 간 smoothing 기법
- DI-MatMul => dynamic하게 quantize를 해서 matmul
- DI-ClippedSoftmax, DI-Exp, DI-Norm => dynamic하게 quantize를 해서 복잡한 non-lienar operation도 잘 했다
Related Works
이미 앞선 게시물에서도 많이 다뤘으니 가볍게 넘어갑시다요
- weight-only, weight-activation quantization 이 있고
- softmax, normalization, SiLU 같은 non linear operator는 부분적으로 FP로 처리하더라
- integer only pipeline도 등장했으나 CNN 같이 다른 아키텍쳐거나 I-BERT의 경우 L1 layer Norm, 그리고 일부 nonlinear op만 다항식 근사를 통해 해결했다 (+일부 INT32), I-ViT는 LLM과 성질이 다르고 마찬가지로 INT32를 사용한다

- 현대 LLM에 더 적합한 형태로 바꿔야 한다, 또한 computational graph 전체에서 INT8 혹은 lower만 사용하는 게 좋겠다 (모델 weight가 커지면서 high-precision은 overhead가 상당하므로)
- activation scale은 좀 더 dynamic하다, smoothing 없이 마냥 quantize 하면 안된다

Quantization (Uniform, but asymmetric)

- (14) 처럼 scale factor를 구하고, (13) 처럼 quantize를 한다 (n = bits to use for quantization)
- (15) 처럼 zero point(bias)를 구해둬야 함, 실수 0에 대응되는 quantized val, (16)처럼 dequantize를 한다 (zp 빼야함)
Fully-Smooth Block-Reconstruction (FSBR)
Notation
* x^I (int), x (fp), Q (quant func),⌊·⌋ (floor), ⌊·⌉ (rounding), ⊗ (element-wise multip), ⊘ (element-wise div)
FSBR
* activation과 weight을 평탄화하는 smoothing coefficient를 학습해서 channel-level로 평탄화 작업(변형)을 수행하자

LLM block에는 여러 타입의 building block이 있다:
- parallel linear-linear, serial linear-norm, serial linear-linear, nonlinear act-smooth
- 최종 결과를 바꾸지 않으면서 channel-wise smoothing을 적용하는 방법은 한쪽에는 s (smoothing factor)를 곱하고, 한쪽에는 s로 나눠 variance를 줄이는 것이다
- 한 채널이 서로 다른 병렬/직렬/비선형 활성화 경로들을 통과할 때 variance가 커지는 걸 방지
cf) SwiGLU 처럼 gated activation function이 포함되어 있다면? 단순히 linear transform은 불가

x1 = xW + b, x2 = xV + c
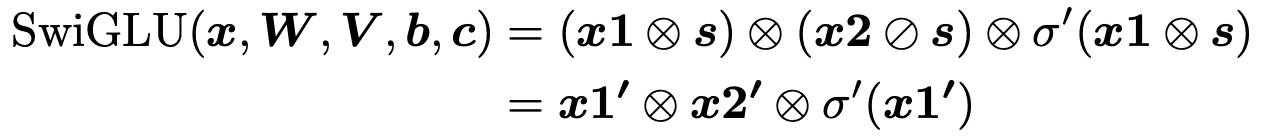
W′ =W ⊗s, b′ =b⊗s, V′ =V ⊘s, c′ =c⊘s,x1′ =xW′ +b′, x2′ = xV ′ + c′, σ′(x1′) = σ(x1′ ⊘ s)

이런 식으로 forward inference process 가능
=> SmoothQuant, OmniQuant와 비슷한 방법
Dynamic Interger-only MatMul (DI-MatMul)
cf) dyaic number란 "정수 / 2의 거듭제곱 꼴의 숫자" 를 말함, fp 연산을 정수 산술 + bit shift로 대체하기 위해 고안된 기법

model의 activation은 dynamic 하므로 runtime 내내 fixed된 quantization parameter를 가지는 것보다 dynamic하게 계산해야 함


s_1, s_2, s_y : floating-point scalar 값, quantization step size를 의미, dyadic number로 근사할 수 있다 (k, m 모두 8bit)
zp1, zp2, zp : zero-point, 실수 0에 대응되는 quantization value

matrix multiplication을 통해 원래 output Y는 다음과 같이 구할 수 있음
- X1, X2 를 zp에 대해 보정하고, 실제값/S 에 대응되는 정수로 만듦 => 그리고 scale s1, s2를 곱하면 최종 fp result Y의 근사값 나옴!!
우리는 이 Y를 계속 양자화해서 가지고 있고 싶다 => 대신 dynamic하게 quantization parameter를 계산해서 !
Y의 scale s_y는 다음과 같이 (data 분포를 고려한 step size, P^I의 max-min 을 균등하게 나누는) * s1 * s2 로 구할 수 있겠지
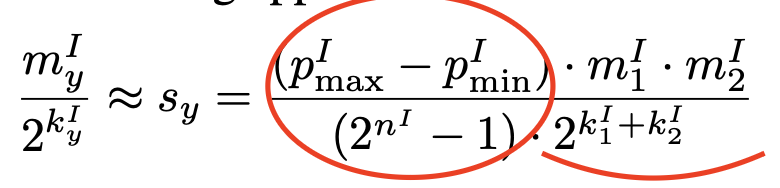
이런 m_y, k_y quantization parameter를 구하는 문제로 귀결된다

저자들은 이 optimization equation을 풀기 위해

1) m_y를 256으로 고정 후 optimal k_y를 찾고 (단조 함수므로 local minimum = global minimum, 찾는 순간 멈춰도 됨)
2) k_y를 기반으로 m_y 값을 찾는다
=> 이 m_y, k_y는 이후 dequantize 시 scaling factor로 사용된다
// 참고로 floor(log2( )) 연산은 MSB method나 right shift로 처리 가능

output 압축은 다시 이런 형태로 진행된다
=> inference 도중 per-token, per-batch dynamic quantization이 가능하다~
Dynamic Interger-only Clipped Softmax
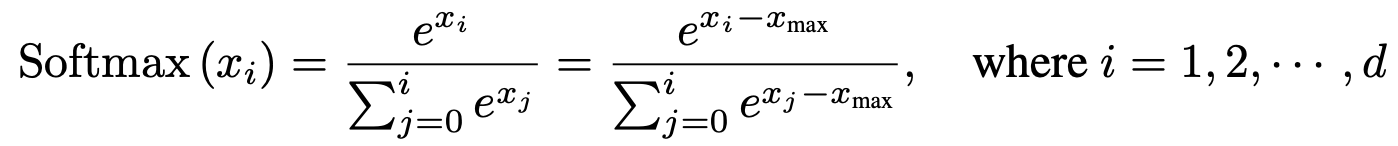
numerical stability를 위해 x_max를 뺀다, x_i <= x_max - 20 이면 exponential 취한 값을 0으로 취급해도 무방하더라
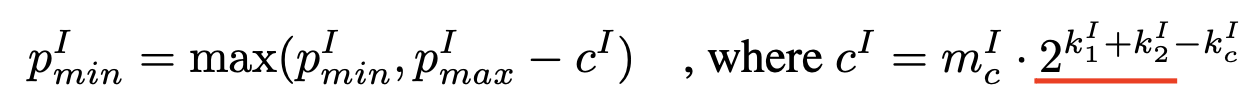
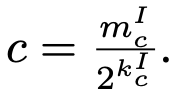
여기서 아이디어를 얻어 single token의 quatization range를 (x_max-c, ) 로 제한하자, c는 dyadic number
c는 실수 도메인에서 clipping하고 싶은 softmax 입력 구간의 길이
=> quantized된 범위의 c^I 로 변환하려면 scale s1, s2로 나누어줘야 함, 그래서 2^k1 와 2^k2가 곱해진 것
=> 이렇게 한다면 quantization range가 c를 exeed 하지 않을 것
저자들이 찾은 값으론 c=15에서 quant error가 0.047을 넘지 않으면서 적절했다고 함

Dynamic Integer-only Exponent function
non-linear exponential 연산도 shift operation만으로 할 수 있다

x를 x_I 와 scale (dyaic number m_x, k_x 로 표현), shift 연산을 위해서 밑을 2로 바꾸고 log_2(e) 도입

x를 정수부(1로 나눈 몫) + 소수부(1로 나눈 나머지)로 표현 가능, integer quantized된 상태에서 정수부를 구하려면 1/s scale down된 s_I로 나눠줘야 함, 소수부는 나머지에 다시 s를 곱해 scale up 해야겠지


r^I * s 는 소수부에 해당하기에 (-1,0) 사이 범위고, 더 간단히 선형으로 근사 가능 => 최종적인 근사식은 다음과 같다
(taylor 전개, 2차 함수 fitting 보다 더 간단한 방식이라고 저자들이 주장)
사실 approximation이 많이 들어가서 얼마나 accuracy drop이 있을진 모르겠지만..

Dynamic Interger-only Normalization
RMSNorm은 LayerNorm보다는 간단한 버전이다, mean/bias 구할 필요가 없음
RMSNorm은 centering step이 없기 때문에 channel간 차이가 더욱 극심하기도 함 => 채널 간 fluctuation을 잡아주어야 함
* FSBR을 수행하여 Norm layer input에 대해 per-channel quantization 을 수행한다
* 추론 시, mean은 쉽게 구할 수 있고, variance 구할 때 root mean square 함수는 I-BERT에서 사용한 Newton 방식 대신 bit-wise check method를 사용했다 (훈련 때 쓰던 정확한 제곱근을 복원하도록)


고전적인 기법이라고 함
Dynamic Interger-only SwiGLU
앞선 block reconsturciton stage에서 non-linear smoothing을 위해 SwiGLU 를 SiLU * x 로 분해했었음
- sigmoid nonlinearlity는 DI-Exp 연산자를 활용해 구하고
- 두 개의 integer multiplication 연산을 합치면 됨

Experiments
non-linear operator의 activation은 전부 INT8 유지
linear operator의 weight/activation 은 configuration에 따라 INT4, INT8 ...
(라고 했는데 table 보면 아닌거같기도, 전부 configuration)
타겟 모델은 오픈소스 LLM = OPT, LLaMA, LLaMA2, LLaMA3-8B
dataset은 WikiText2, C4 (perplexity를 측정함) , PIQA, ARC, BoolQ, HellaSwag, Winogrande (zero-shot accuracy)
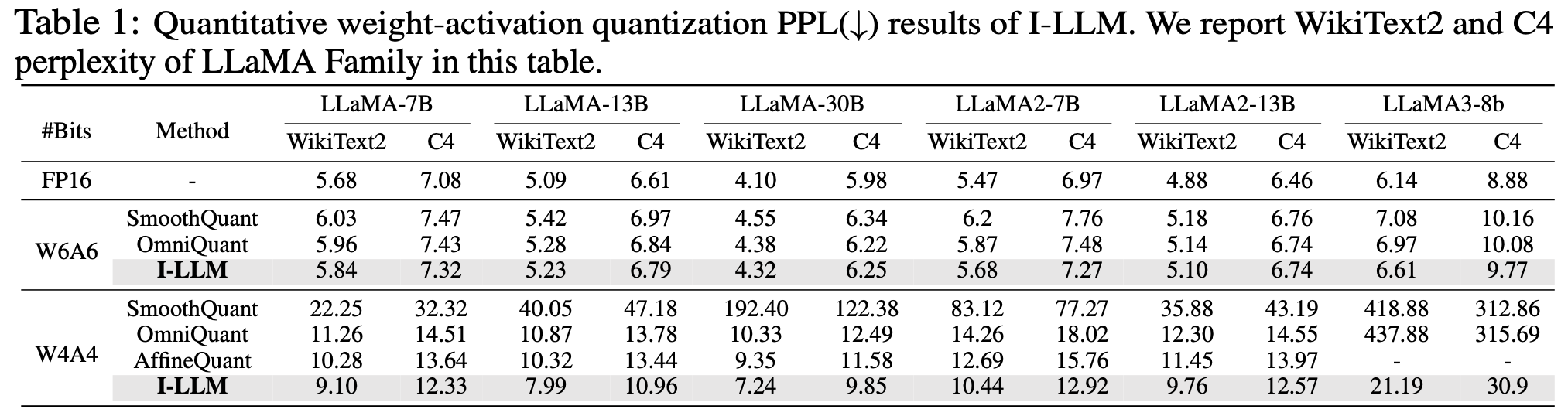
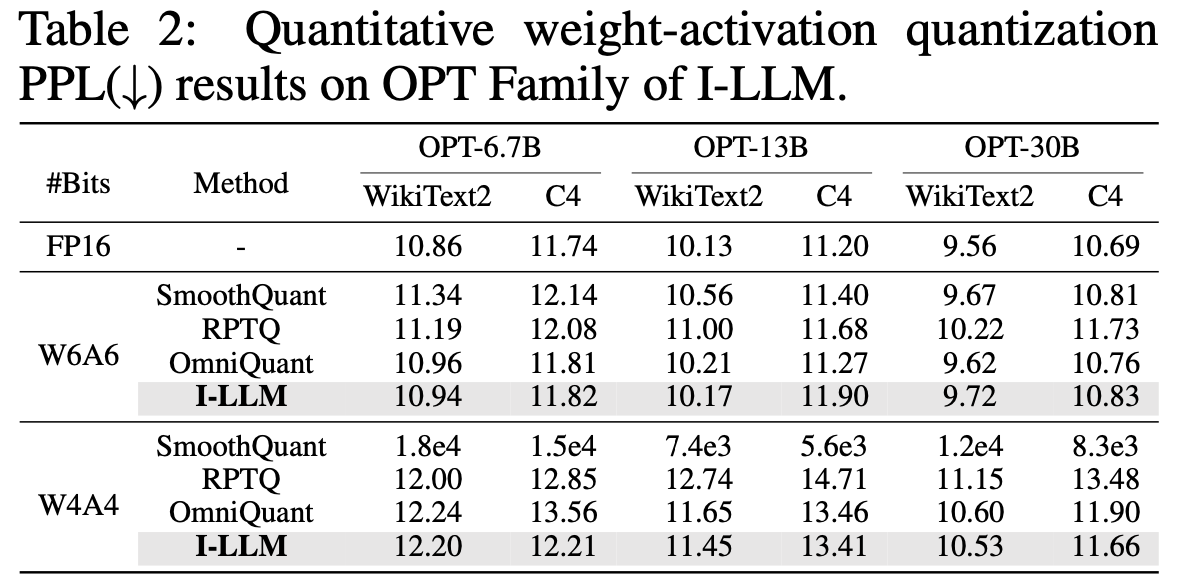
Ablation study

FSBR이 비슷한 idea를 가진 SmoothQuant, Omniquant 보다 좋더라
why? 기존 기법은 non-linear layer의 activation을 그대로 quantize했고, 성능에 악영향을 줬다
코드 구현
(구현된 것)
- 캘리브레이션 데이터에 대해 샘플링(channel별 최대치(scale)/평균(shift) 뽑아서 저장)
- 각 블록의 channel-wise scale/shift를 learnable parameter로 등록하고 MSE 최소화하도록 학습
- QuantLinear wrapper module: weight/activation을 UniformAffineQuantizer로 fake-quantize 및 dequantize
- UniformAffineQuantizer = per-tensor/per-channel 에서 static/dynamic 방식으로 scale 및 zero point 결정, float → quant → dequant → float 를 forward마다 실행하여 양자화 오차는 측정 가능
(구현안된 것)
- integer-only operator: 여전히 F.sigmoid, F.softmax, layer_norm, torch.rsqrt 등 비선형 연산을 그대로 사용하고, 부동소수점으로 처리하는 중 => 양자화 오차 시뮬레이션만 하고 있음
(총평)
알고리즘은 (어느정도는) 이해하겠으나 1) 기존 방법론을 그대로 가져온 느낌이거나 2) 다르게 갔으나 이런 approximation이 진짜 성능 저하 없이 효과적인지 모르겠음
코드에서 FSBR 부분은 구현이 되어있으나 논문의 핵심 부분인 integer operator가 하나도 구현 안되어있어서 아쉬움