GNN에서의 convolution

https://distill.pub/2021/understanding-gnns/

Understanding Convolutions on Graphs

과거에는 그래프 분석에 graph kernel과 random-walk 기법이 사용되었다

• 계산량이 많고, 알고리즘 기반으로 그래프의 구조적 특성을 미리 설계된 규칙(예: 서브트리, 최단 경로, 랜덤 워크 경로 등)을 활용해 추출하는 방식

현재는 GNN으로 대체되었다

• 데이터로부터 end-to-end 학습을 통해 입력 그래프의 노드, 엣지, 글로벌 속성 간의 복잡한 상호작용을 자동으로 모델링하는 방식

graph는 특수한 성질을 가지고 있다

- lack of consistent structure (극한으로 flexible한 수학적 모델이다)

- no inherent ordering among the nodes (node order가 상관없다, permutation invariant)

- 매우 크다, 하지만 sparse한 성질을 가진다

 

다음과 같은 task에 사용된다

- node classification

- graph classification

- node clustering

- link prediction

- influence maximization (indentify influential nodes?)

 

Local Convolution - Polynomial Filters on Graphs

local convolution 방식에 대해 알아보자. locally neighborhood의 정보를 가져와 본인을 update 하는 방식이다

 

polynomial filters

adjacency matrix A에 대해 diagonal matrix D를 위와 같이 정의할 때, graph laplacian matrix L = D - A

cf) 왜 이런 form을 사용하냐?

- positive semidefinite matrix라 수학적으로 유용함

- 그래프의 smoothness와 관련 있음, 그래프적으로 인접 노드와의 변화/차이 를 나타냄

 

polynomials of the Laplacian을 위와 같이 설정할 수 있다.

coefficient vector w는 d-dim 일 것이고, p_w(L) 역시 nxn matrix일 것이다

feature vector x (n*d = num_node * feature_dim)의 convolution은 위와 같이 정의할 수 있다

 

이 polynomail은 CNN에서의 "filter"로 해석 가능하다. why?

L^i 에서 0인 element들은 v,u의 거리가 i 초과임을 알 수 있다, i-hop에 포함되지 않는다

x_v (x의 v번째 row, node v의 feature vector)

즉 이 polynomial filter를 적용하면 d hops 이하의 node u에 대해서만 영향을 받는다, image convolution filter와 비슷한 느낌

 

ChebNet

polynomial filter의 개선된 버전, T_i는 Chebyshev polynormial of first kind의 i번째 degree

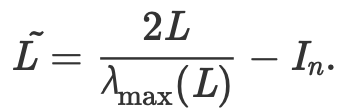
L을 normalize함으로써 L의 eighenvalue를 [0,) → [0,2] → [-1,1] 범위로 scale-down 했다, L이 곱해질 때 explode하지 않음 !!

 

polynomail filter is permutation-invariant

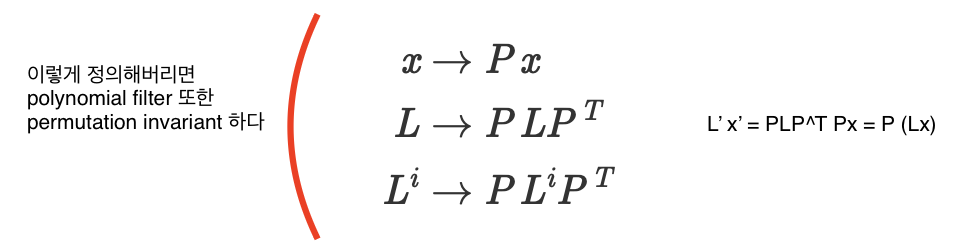
permutation matrix P (PP^T = I) 에 대해 위와 같이 세팅하면 f(Px) = Pf(x) 을 만족한다

 

embedding computation

ChevNet 혹은 polynomial filter 레이어와 nonlinearlities를 쌓는다면 GNN을 만들 수 있다

polynomial filter를 계산하고 -> h에다가 filter를 적용하고 → non linearlity를 적용

서로 다른 node에 대해 동일한 filter weight를 재사용, filter weight = learnable parameters

 

Modern GNN에서의 embedding computation

local convolution은 인접 노드들의 feature를 aggregate 하고 → 자신의 feature와 combine 하는 형태를 띤다

"message passing" 방식 = 각 step마다 이웃들로부터 어떤 정보를 받는다 / receptive field = K hops away

 

Graph Convolutional Networks (GCN)

Graph Attention Networks (GAT)

Graph Sample and Aggregate (GraphSAGE)

Graph Isomorphism Network (GIN)

당연히 node들에 대한 연산 + edge 연산도 하는 모델들도 많다

 

Importance of Graph Laplacian L

-주어진 graph G에 대해 feature vector x가 얼마나 smooth한지 보여준다

위와 같은 objective function을 설정했을 때, feature vector x가 인접한 노드들에 대해서는 비슷한 값을, 멀리 떨어진 노드들에는 다른 값을 배치했을 경우 R_L(x)이 작아짐

 

Global Convolutions?

위에는 "local convolution" 이다 = every node feature는 local neighbor의 feature를 바탕으로 업데이트 됨.

하지만, global한 정보를 볼 수 있게 convolution을 짠다면??

 

spectral convolutions

L은 positive semidefinite matrix 이므로 spectral decomposition이 가능하다 (lambda_1 <= ... <= lambda_n)

u_1, ... u_i-1 번째 기저벡터까지 선택한 상황에서, R_L(x)은 x=u_i 에서 lambda_i 라는 최솟값을 가진다

 

즉 global convolution은

U^T x를 통해 x를 eigenvector를 기저로 하는 좌표계로 변환시킨 후

x_hat 에서 첫번째 m개의 component만 남기고 나머지는 truncate를 하고 = eigenvalue가 작은 저주파 부분만 남기고

다시 natural representation 좌표계로 변환한다

 

cf) vs. PCA

- PCA는 covariance matrix에서 고유값이 큰 축(고유벡터)만 남기고 truncate

- 주성분 (가장 분산이 큰 축) 데이터만 남긴다

- 반면에 global convolution은 L을 분해한 뒤 고유값이 작은 축만 남기고 truncate

- 그래프에서 부드러운 성분만 남기는 효과 = 인접 노드는 비슷한 값(=부드러운 신호)을 최대한 잘 표현하게

 

spectral convolution의 임베딩 연산

- 한 layer당 필요한 weight 수는 m (= spectral representation을 계산하는데 필요한 eigenvector 수)

- 연산을 위해 graph Laplacian L을 계산하고, 분해해서 U를 구해야 함

- 당연히 이 연산도 node-order quivariant하다 = permutation invariant

 

spectral convolution의 한계

큰 그래프에 대해서는 L을 분해하여 U를 구하는게 비싸다

U를 구한다 하더라도 여전히 U^T, U matrix multiplication 연산도 비싸다

learned filter (w)는 특정 spectral decomposition에 대해 표현된다, 새로운 형태의 graph에 잘 적용되지 않는다

 

따라서 graph-level information을 얻고 싶다면 global convolution을 사용하지 말고 pooling을 사용하자

- node/edge 임베딩을 pooling하여 graph embedding을 우선 계산한 뒤

- iterative하게 node embedding을 update할 때 graph embedding까지 고려하게 하는거지

- 그러면 각 노드들이 전역적인 정보를 어느정도 학습할 것

 

How to set Loss function for training?

1. node classification

2. link prediction

등등