23.06.24 Dreamhack CTF Season 3 Round #6 (🌱Div2) 문제이자 나의 첫 암호학 문제!
Caesar 암호
평문의 각 알파벳을 일정한 거리만큼 밀어서 다른 알파벳으로 치환하는 단일 문자 치환 암호

- 알파벳 소문자만 +13 옾셋만큼 밀어서 치환하더라
RSA 암호
1. 배경지식

φ(n)는 오일러 파이 함수로, n 이하의 양의 정수 중 n과 서로소인 수의 개수
2. 키 생성
- 서로 다른 두 소수 p, q를 선택하여 n=p*q로 세팅한다
- 이 때 φ(n) = p*q - p - q + 1 = (p-1)(q-1) 이다
- φ(n)보다 작은 수 중 φ(n)와 서로소인 e를 선택한다
- d ≡ e^(-1) (mod φ(n)) 를 만족하는 적절한 d를 선택한다
=> n, e 는 공개키로, d는 개인키로 사용한다
3. 암호화 복호화
- 공개키 (n,e)로 평문 m을 암호화하는 방식은 다음과 같다 (m<n)

- 개인키 d로 암호문 c를 복호화하는 방식은 다음과 같다

// 증명은 오일러 정리로 할 수 있다

AES 암호
AES는 SPN(Substitution Permutation Network)이라는 암호 구조를 사용한다
S-Box를 사용하는 치환(Substitution)과 P-Box를 사용하는 순열(Permutation)을 여러 라운드에 걸쳐 반복
AES는 라운드마다 128비트 크기의 블록을 암호화하는 블록 암호 = 각 칸이 1Byte인 4행 4열의 블록
블록 상태로 재구성된 입력에 대해 AddRoundKey 함수를 적용하고,
마지막 라운드 전까지 매 라운드마다 SubBytes, ShiftRows, MixColumns, AddRoundKey 함수를 반복하여 적용
마지막 라운드에는 SubBytes, ShiftRows, AddRoundKey 함수 적용
=> 각 라운드의 함수들은 역함수가 존재하므로, AES 복호화도 가능하다!
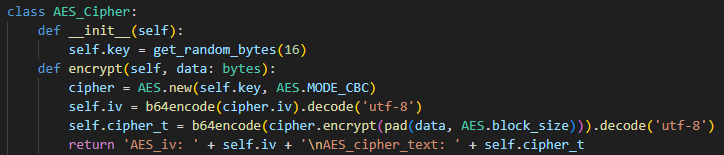
- key: 랜덤 16바이트, base64 인코딩 된 initialization vector와 cipher_text를 출력해준다
- key, iv, cipher_text만 있으면 AES 복호화 가능하겠다
코드 분석

- AES 암호화에 사용되는 key를 big endian 형태로 받아와 ac_key에 저장하고 있다
- 상위 7바이트 RSA 암호화한 결과를 "Key1: " 뒤에 출력해주고
- 하위 9바이트 카이사르 암호화한 결과를 "Key2: " 뒤에 출력해줌

=> 두가지 암호화를 복호화하여 key를 복원하고, AES 복호화 진행한다
문제 풀이
1. caesar_cipher
class Caesar_Cipher:
// 생략
def decrypt(self, data: str):
cipher_t = [i for i in range(len(data))]
for i in range(len(data)):
ch = data[i]
if(ch in self.alpha):
idx = self.alpha.index(ch)
cipher_t[i] = self.alpha[(idx - 13 + 26) % 26]
else:
cipher_t[i] = ch
return ''.join(cipher_t)encrypt 함수를 약간 변형해서 decrypt 만들기만 하면 된다
2. RSA_cipher
def get_divisor():
# n = 3573716833 * 3671005097
n = 13119132709177697801
for i in range(1,3622034333): # sqrt(b) = 3622034332.965067
if n%i==0:
print(i)
def calc_pi():
# 13119132701932975872
print((3573716833-1)*(3671005097-1))
def get_d():
# 1803412828046968577
e = 65537
pi_n = 13119132701932975872
for i in range(1,10000):
tmp = pi_n * i + 1
if tmp%e==0:
print(tmp//e)큰 수 계산에 능한 python을 사용해 개인키 d를 구하고
class RSA_Cipher:
// 생략
def decrypt(self, data: int):
d = 1803412828046968577
cipher_n = pow(data, d, self.n)
return cipher_ndecrypt 함수를 구현했다
3. AES_cipher
class AES_Cipher:
def __init__(self):
self.key = get_random_bytes(16)
def encrypt(self, data: bytes):
cipher = AES.new(self.key, AES.MODE_CBC)
self.iv = b64encode(cipher.iv).decode('utf-8')
self.cipher_t = b64encode(cipher.encrypt(pad(data, AES.block_size))).decode('utf-8')
return 'AES_iv: ' + self.iv + '\nAES_cipher_text: ' + self.cipher_t
def decrypt(self, data, key, iv):
data = b64decode(data)
iv = b64decode(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(data)
return unpad(flag, AES.block_size).decode('utf-8')encrypt 함수에서
- cipher_t / iv 를 base64 인코딩했으니 다시 b64decode 해야 되고
- pad(data, AES.block_size) 했으니 다시 unpad(data, AES.block_size) 해야 되겠지
rc_p = rc.decrypt(int('69173442be2ea6a7', 16))
print("Decrypt_key1: ", hex(rc_p)[2:])
cc_p = cc.decrypt('q7r6srq6r515ro294s')
print("Decrypt_key2: ", cc_p)
org_key = hex(rc_p)[:] + cc_p
org_key = int(org_key, 16)
byte_key = org_key.to_bytes(16, 'big')
print(ac.decrypt('NbQVjxyfejY/Pzxm/Jscn3ATi94wdVst9YDCtIysGCE74F/VGuldQ1oLtM2+Pzh1+cEB3DQZcUz0VCO1/skBfEXRfnzYWFuKoIk5caxhCGM=', byte_key, 'dkknruN2ybiXmszkJxG3EA=='))
그러면 플래그 나온다 끗!
'security > 암호학' 카테고리의 다른 글
| 확장된 유클리드 호제법 구현 in python (0) | 2023.08.20 |
|---|---|
| RSA 암호화 알고리즘 정리 및 예제 (feat SSTF 2023) (0) | 2023.08.20 |
| RC4 암호화 알고리즘 정리 및 예제 (feat SSTF2023) (1) | 2023.08.20 |
| AES 암호화 알고리즘 정리 및 예제 (feat SSFT 2023) (0) | 2023.08.20 |
| [Blitzs CTF] d + 파이썬 itertools!! (0) | 2023.06.25 |