RSA 암호화 알고리즘이란
- modular exponentiation operation 기반으로 한 암호화 알고리즘
- n과 e를 공개키로, d를 개인키로 사용하여 아래와 같이 exponentiation을 통해 암호화 및 복호화 한다

- key generaton 방식은 아래와 같다

// 먼저 적절한 소수 p와 q를 선택하여 n을 구한다

// e를 적절히 선택하고, 개인키 d를 역산한다
// 만약 attacker가 p, q, d 중 하나를 찾는다면 모든 ciphertext에 대해 decrypt가 가능할 것이다
취약점 분석 예제 1
from sympy import randprime, nextprime
from secret import pt
p = randprime(pow(2, 511), pow(2, 512))
q = nextprime(p)
n = p * q
e = 65537
ct = pow(pt, e, n)
print("n =", hex(n))
print("ct =", hex(ct))
'''
$ python3 challenge.py
n = 0xa28c55dd2df4f6845a1faf7755c080acf59da763174cf1cfddf87eaa4ba80dadfa7f26fe067fa319c002b750ac4b1b60d840efb0f340db4cd7fabafd9105a4cb4a5e8172da56750cd05343c7d294051ab506cf1040bd4f091e5c8efeb88fe83f96da1a8554a84c3db6d17a2f78fd0d17ecd09880df3c91b3aa85ad342b45b7e3
ct = 0x19cea145a7495409a0ab504261b80e9f404b030635d6d342b5efd541c11adfcdaa6c091051be0fcfac2c475d74853169c463b22c1ab9d053ed37bbe8dc4d3605f6cf2ef0d43947d62f5966b5188db03bf93b220185f3c7a1e4eae39c023410e824fae00ff3c8b015dbb63e876a0a79347c5bd611efc7bccd8471ad926d3b7807
'''- 공개키 n과 e, 그리고 ct가 공개되어있다.
- p와 q는 연속된 소수이므로 비슷할 것, 제곱근 n 근처에서 p와 q를 찾을 수 있을 것이다
- p나 q 파악 시 비밀키 d 역시 파악 가능하므로 decryption 가능하다
매우 큰 정수의 정수 제곱근 구할 때 => gmpy2 의 isqrt 함수 사용하자
from gmpy2 import isqrt
n = 0xa28c5~~
ct = 0x19cea145a7~~
e = 65537
q = isqrt(n) # integer square root of n
while n%q!=0:
q += 1
p = n//q
sig_n = (p-1)*(q-1)
d = pow(e, -1, sig_n)
pt = pow(ct, d, n)
pt = bytes.fromhex(str(hex(pt))[2:])
print(pt)
취약점 분석 예제 2
from base64 import b64encode, b64decode
from Crypto.Util.number import getStrongPrime, bytes_to_long, long_to_bytes
from os import system
p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
e = 65537
d = pow(e, -1, (p - 1) * (q - 1))
print("[RSA parameters]")
print("n =", hex(n))
print("e =", hex(e))
def sign(msg):
m = bytes_to_long(msg)
s = pow(m, d, n)
return long_to_bytes(s)
def verify(s):
s = bytes_to_long(s)
v = pow(s, e, n)
return long_to_bytes(v)
def welcome():
print("\nWelcome to command signer/executor.")
print("Menu : 1. Verify and run the signed command")
print(" 2. Generate a signed command")
print(" 3. Base64 encoder")
print(" 4. Exit")
while True:
welcome()
sel = input(" > ").strip()
if sel == "1":
sgn = input("Signed command: ").strip()
sgn = b64decode(sgn)
cmd = verify(sgn)
commands = ["ls -l", "pwd", "id", "cat flag"]
if cmd.decode() in commands:
system(cmd)
else:
print("Possible commands: ", commands)
elif sel == "2":
cmd = input("Base64 encoded command to sign: ")
cmd = b64decode(cmd)
if cmd == b"cat flag":
print("It's forbidden.")
else:
print("Signed command:", b64encode(sign(cmd)).decode())
elif sel == "3":
cmd = input("String to encode: ").strip().encode()
print("Base64 encoded string:", b64encode(cmd).decode())
elif sel == "4":
print("bye.")
exit()
else:
print("Invalid selection.")- 2번 옵션 : 원하는 입력에 대해 signed된 결과를 받을 수 있다
- 1번 옵션 : signed command를 입력하면 verify 후 특정 조건에서 커맨드를 수행해준다
- 개인키로 sign 하고, 해당 sign이 유효한지 공개키로 verify 하는 형태.
=> 우리는 "cat flag" 커맨드의 sign 값을 알아야 한다. 하지만 sign 값을 획득하는 루틴인 2번은 b'cat flag' 막아둠

=> C를 C1, C2로 decomposition 후 각각에 대한 sign 값 M1, M2를 만들고 둘을 다시 combine 하면 C에 대한 sign 값 획득!
from pwn import *
from base64 import b64encode, b64decode
from Crypto.Util.number import bytes_to_long, long_to_bytes
p = remote("rsa101.sstf.site", 1104)
def menu2(text):
p.recvuntil("4. Exit\n > ")
p.sendline("2")
p.sendline(text)
p.recvuntil("Signed command: ")
return p.recvline()[:-1]
def menu1(text):
p.recvuntil("4. Exit\n > ")
p.sendline("1")
p.sendline(text)
C = bytes_to_long(b'cat flag')
C1 = 2
while C%C1!=0:
C1 += 1
C2 = C//C1 # C = 103 * 69525558883514113
p.recvuntil("n = ")
n = int(p.recvline()[:-1], 16)
C1_b64 = b64encode(long_to_bytes(C1))
C2_b64 = b64encode(long_to_bytes(C2))
M1 = b64decode(menu2(C1_b64)) # signed command of C1
M2 = b64decode(menu2(C2_b64)) # signed command of C2
M = (bytes_to_long(M1)*bytes_to_long(M2)) % n # signed command of b'cat flag'
signed = b64encode(long_to_bytes(M))
menu1(signed)
p.interactive() # SCTF{Mult1PLIc4t1v3_pr0pErty_of_RSA}// b64encode & decode 가 많고 bytes<->long 변환 많아서 복잡하긴 하네
만약 cypertext C가 factorize 안된다면?

// 임의의 정수 a를 곱한 후 factorize 해서 동일한 방식으로 exploit
취약점 분석 예제 3
from secret import notice
from Crypto.Util.number import bytes_to_long as b2l
pubkeys = dict()
#Alice's RSA public key
pubkeys['Alice'] = {'n': 0xd244a731d125aa8cbbccc5aa44b70686b432589d7a472269059055119e258e471df27d0f08c3c5e109829381754745f47b6bb3a5e3cc5a3b63766aa8c929290596de12234c244d6746398cc81f774441946c6d0444ce23ab146c33876cf84dc122eb0d42c4437e969ad8b72fbc399c82abd2e153e8d27dff56f517c5cb980853, 'e': 79}
#Bob's RSA public key
pubkeys['Bob'] = {'n': 0xd244a731d125aa8cbbccc5aa44b70686b432589d7a472269059055119e258e471df27d0f08c3c5e109829381754745f47b6bb3a5e3cc5a3b63766aa8c929290596de12234c244d6746398cc81f774441946c6d0444ce23ab146c33876cf84dc122eb0d42c4437e969ad8b72fbc399c82abd2e153e8d27dff56f517c5cb980853, 'e': 61}
def send_notices(addr, msg):
msg = b2l(msg)
print(msg)
for recipient, keypair in addr.items():
#RSA encryption
ct = pow(msg, keypair['e'], keypair['n'])
print("{} <- {}".format(recipient, hex(ct)))
send_notices(pubkeys, notice)
'''
$ python3 challenge.py
Alice <- 0x55edc128e01d6a94d92482d4136a60c5db5e295aec9c38e4029649bfc42eb350cf3ccdddc101c5a81d1251f9b061fe55b436eaba101b0238db479e795661ad64dd0e04898bdd637d33b15c155d1141e70efc84923c126f7d93582d5783544780c9a29818a8f47bad2e47967f7609aa3e6caabbd153c77def6d20e7ed4ac267a8
Bob <- 0xcad43d8d2bcb9ab05133e0923896426544fd8a93e80e0b10efc36019b8a7365390b30530f240b25d3affa6ed03983548fe17f085fe3f04a6bd80aa9093eda484e7c9a120e770000570a2044f7aa6ea5dc25ef082c352205f710b07423160b70f100800d3dedf89843a19208054550f22936fe510e7a98fe1c557b7657abfb77b
'''- 동일한 메시지(notice)에 대해 Alice와 Bob이 각각 RSA 암호화 한 ciphertext를 출력해준다
- n은 동일하고 e만 다른 상황
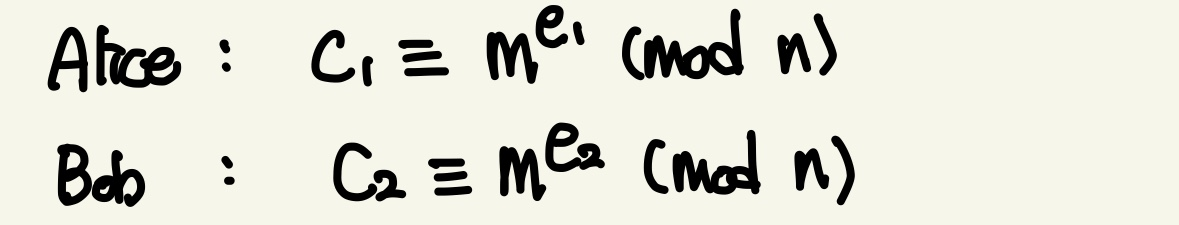
- 우리는 (C1, e1, C2, e2, m)을 알고 있다
- 확장된 유클리드 호제법에 의해 s*e1 + t*e2 = gcd(e1,e2) = 1을 만족하는 s,t 가 존재한다
- e1=79, e2=61에서 s=17, t=-22이다

- m을 쉽게 구할 수 있겠다
from Crypto.Util.number import long_to_bytes
from gmpy2 import gcdext
n = 0xd244a73~~
c1 = 0x55edc128edd ~~
c2 = 0xcad43d8d2bcb ~~
gcd, s, t = gcdext(79, 61)
msg = (pow(c1,s,n) * pow(c2,t,n)) % n
print(long_to_bytes(msg))'security > 암호학' 카테고리의 다른 글
| DSA 전자 서명 (feat. Textbook-DSA) (0) | 2023.09.06 |
|---|---|
| 확장된 유클리드 호제법 구현 in python (0) | 2023.08.20 |
| RC4 암호화 알고리즘 정리 및 예제 (feat SSTF2023) (1) | 2023.08.20 |
| AES 암호화 알고리즘 정리 및 예제 (feat SSFT 2023) (0) | 2023.08.20 |
| [Blitzs CTF] d + 파이썬 itertools!! (0) | 2023.06.25 |